Дистанційна освіта з інформатики 01.02.2021 - 07.02.2021

 Дистанційна освіта з інформатики в період лютого  2021 року

01.02.2021 - 07.02.2021

Конспект уроку для учнів

 

Тема: Середовище опису та виконання лінійних та нелінійних алгоритмів Скретч.

Теоретична частина

Фізкультхвилинка

Один, два – усі піднялись,

Повернулись, похитались.

Три, чотири – руки вгору,

В сторони і вгору знову.

П’ять, шість – опустили,

І швиденько всі присіли.

Сім, вісім – всі малята

Стрибають, як жабенята.

Дев’ять, десять, - рівно стали

І за парти посідали.

 

 

 

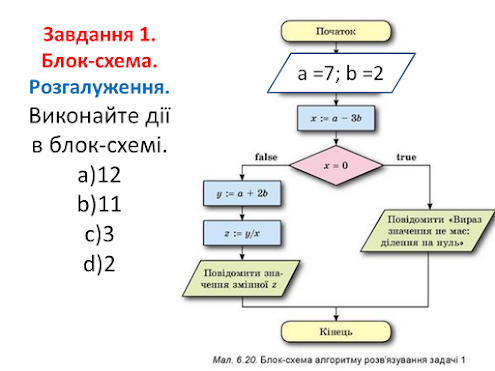
Осмислюємо властивості алгоритмів 

на текстовому матеріалі різнорівневих

 компетентнісних завдань:

 

Зразок 1.
Створити алгоритм для складання магічних числових стовпців Вінницького вигляду:
а  ... а ... а ... а ... а = 0
а  ... а ... а ... а ... а = 1
а  ... а ... а ... а ... а = 2
а  ... а ... а ... а ... а = 3
а  ... а ... а ... а ... а = 4
................
а  ... а ... а ... а ... а = n-2
а  ... а ... а ... а ... а = n-1
а  ... а ... а ... а ... а = n

Де замість знаку «...» можна нічого не ставити а дозволяється поставити будь-яку арифметичну дію: додавання, віднімання, множення, ділення. А також у виразі можна поставити: круглі дужки, квадратні дужки- це ціла частина від дробового числа, фігурні дужки - це дробова частина від будь-якого числа, можна поставити квадратний корінь, можна поставити дію факторіал числа.

Реалізація.
Алгоритм матиме такі команди:
(а -а)*а*а*а = 0
а:а+(а-а)*а =1
(а+а):а+а-а=2
(а+а):а+а:а=3
(а+а+а+а):а=4
.............
а-а:а-а:а=а-2
а-а:а+а-а=а-1
а+а-а+а-а=а
аа:аа+а=1+а
а:а+а:а+а:а=2+а
.......... і так далі.

Зразок 2.
Створити алгоритм для складання чарівних числових стовпців Вінницького такого вигляду:
1 ... 2 ... 3 ...    ... 8 ... 9 = 0
1 ... 2 ... 3 ...     ... 8 ... 9 = 1
1 ... 2 ... 3 ...     ... 8 ... 9 = 2
1 ... 2 ... 3 ...     ... 8 ... 9  = 3
1 ... 2 ... 3 ...     ... 8 ... 9 = 4 
................. і так далі

Де замість знаку ... можна нічого не ставити а дозволяється поставити будь-яку арифметичну дію: додавання, віднімання, множення, ділення. А також у виразі можна поставити: круглі дужки, квадратні дужки- це ціла частина від дробового числа, фігурні дужки - це дробова частина від будь-якого числа, можна поставити квадратний корінь, можна поставити дію факторіал числа.

Реалізація.

Покажимо алгоритми для окремого випадку  n = 100. Тобто
1 ... 2 ... 3 ...    ... 8 ... 9 = 100
Тоді отримаємо більше 10 варіантів:
1*2-3+4-5+6+7+89 =100
1+2+3+4+5+6+7+8*9 =100
(1+2+3-4)*5*6*(7+8):9=100
1+2+3-4+5+6+78+9=100
(1+2):3+4+5-6+7+89=100
1*2+34+56+7-8+9=100
12-3-4+5-6+7+89=100
123+45-67+8-9=100
123-4-5-6-7+8-9=100
123-45-67+89=100
123+4-5+67-89=100
12+3-4+5+67+8+9=100.

 

 

 

Зразок 3.
Створити алгоритм для складання магічного квадрату розміром 3х3 із довільних трьох різних  чисел, які позначені латинськими змінними:
a, b, c. Умова магічності така. Треба щоб у кожному рядку таблиці стояли різні числа, у кожному стовпці таблиці стояли різні числа. А сума чисел кожного рядка дорівнювала добутку чисел кожного стовпця. А сума чисел кожного стовпця дорівнював добутку чисел кожного  рядка.
Реалізація.
Розглянемо таке позначення адресу клітинки в числовій таблиці:
(1; 1)   (1; 2)   (1; 3)    
(2; 1)   (2; 2)   (2; 3)    
(3; 1)   (3; 2)   (3; 3)    
Алгоритм матиме такі команди:
1. Число а поставити в такі комірки квадратної таблиці:
(1; 1)   (2; 3)   (3; 2)   
2. Число  b  поставити в такі комірки квадратної таблиці:
(1; 2)   (2; 4)   (3; 3)   
3. Число c поставити в такі комірки квадратної таблиці:
(1; 3)   (2; 2)   (3; 1)    
Результат.
Утвориться такий квадрат на латинських
буквах.
a  b  c 
b  c  a 
c  a  b
Магічна сума дорівнює a + b+c =S
Магічний добуток дорівнює abc= P
Магічна сума і магічний добуток виконуються як по рядках, так і по стовпцях. Самостійно перевірте цю властивість для двох діагоналей створеного числового квадрата.
Питання, коли виконується умова
a+ b + c = abc,  a=1; b=2; c=3.
1+2+3=1*2*3=6.
Отже, маємо гіпермагічний числовий квадрат 3х3 на сумах і на добутках:
1   2   3
2   3   1
3   1    2  

Зразок 4.
Створити алгоритм для складання магічного квадрату розміром 4х4  із довільних чотирьох різних  чисел, які позначені латинськими змінними:
a, b, c, d. Так щоб у кожному рядку таблиці були стояли різні числа, у кожному стовпці таблиці стояли різні числа.
Реалізація.
Розглянемо таке позначення адресу клітинки в числовій таблиці:
(1; 1)   (1; 2)   (1; 3)     (1; 4)
(2; 1)   (2; 2)   (2; 3)     (2; 4)
(3; 1)   (3; 2)   (3; 3)     (3; 4)
(4; 1)   (4; 2)   (4; 3)     (4; 4)
Алгоритм матиме такі команди:
1. Число а поставити в такі комірки квадратної таблиці:
(1; 1)   (2; 3)   (3; 4)     (4; 2)
2. Число  b  поставити в такі комірки квадратної таблиці:
(1; 2)   (2; 4)   (3; 3)     (4; 1)
3. Число c поставити в такі комірки квадратної таблиці:
(1; 3)   (2; 1)   (3; 2)     (4; 4)
4. Число d поставити в такі комірки квадратної таблиці:
(1; 4)   (2; 4)   (3; 1)     (4; 3) .
Результат.
Утвориться такий квадрат на латинських
буквах.
a  b  c  d
c  d  a  b
d  c  b  a
b  a  d  c
Магічна сума дорівнює a+b+c+d=S
Магічний добуток дорівнює abcd=P
Магічна сума і магічний добуток виконуються як по рядках, так і по стовпцях. Самостійно перевірте цю властивість для двох діагоналей створеного числового квадрата.

Зразок 5.
Створити алгоритм для складання магічного квадрату розміром 4х4  із 16 послідовних натуральних чисел, які позначені латинськими змінними:
a+1, а+2, а+3, ..., а+14, а+15, а+16. Так щоб у кожному рядку таблиці були стояли різні числа, у кожному стовпці таблиці стояли різні числа. Умова магічності така. Треба щоб сума чисел кожного рядка, сума чисел кожного стовпця, сума чисел головної і сума чисел бічної діагоналі дорівнювала числу, яке обчислюється за формулою:       
М=(а+16)(а+17)/8.
Реалізація.
Розглянемо таке позначення адресу клітинки в числовій таблиці:
(1; 1)   (1; 2)   (1; 3)     (1; 4)
(2; 1)   (2; 2)   (2; 3)     (2; 4)
(3; 1)   (3; 2)   (3; 3)     (3; 4)
(4; 1)   (4; 2)   (4; 3)     (4; 4)
Алгоритм матиме такі команди:
1. Заповнюємо цей квадрат підряд, якщо а=0:
1     2     3    4
5     6     7    8
9    10   11  12
13   14   15   16
2. Переставляємо числа тільки на двох діагоналях за правилом. Відносно центру квадрата обмінюються місцями такі пари чисел: 1 і 16;   6 і 11;  7 і 10;   4 і 13.
3. Утвориться такий квадрат на магічний
квадрат на сумах. Якщо а=0:
16     2       3     13
5       11    10     8
9       7        6     12
4       14      15     1
Результат. Магічна сума квадрата 4х4 дорівнює 34.
Магічний добутку у цього квадрата відсутній.
Магічна сума 34 виконуються як по рядках, так і по стовпцях та двох діагоналях.

 

Практична частина.

А тут лежить версія scratch4.30: 

http://scratch.mit.edu/scratch2download/

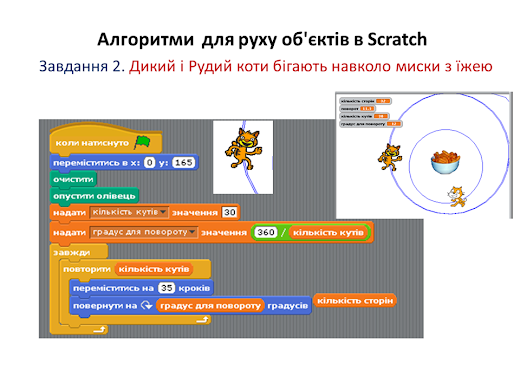
Завдання 1.

Завантажити програму Scratch.  

Відкрити вкладу «Скрипти»

Для Рудого Кота створити алгоритм із скриптів-пазлів в області «Скрипти»

відповідно до поданого зразка.

Протестувати виконання цього алгоритму декілька разів,

для цього треба натиснути на піктограму «зелений прапорець», що розташована  над сценою.

Зберегти цей скретч-проект у файлі з назвою «Алгоритми_ Коло»

 

Результат виконаної практичної роботи це два файла( два скретч-проекти) надіслати вашому учителю на електронну скриньку: 
vinnser@gmail.com (Сергій Петрович)
ktdfz@i.ua (Юрій Васильович)