29.11.2021-05.12.2021
Тема:Алгоритми для знаходження НСК(х;у)
та НСД(х;у)
Теоретична частина
На
множині натуральних чисел виконуються операції додавання і множення, але не завжди виконується операція віднімання. Розширюючи
множину N так, щоб арифметична операція
віднімання завжди виконувалася, ми отримаємо множину цілих чисел Z. Тому Z=N È
{0, -1, -2,...} або множина цілих містить цілі від’ємні
числа(перед від’ємними числами завжди ставлять знак «мінус», нуль(це число, яке немає знаку) та цілі додатні числа(перед додатніми числами ставлять знак
плюс або іноді нічого не ставлять): Z={...-3,
-2, -1, 0, 1, 2, 3,...},
тобто, множина цілих чисел Z містить множину
натуральних чисел, число нуль та числа, які протилежні натуральним(цілі
від’ємні числа).
Зауваження.
Впровадження нуля та від'ємних цілих чисел
здійснено з метою запровадження дії віднімання, оберненої до додавання, так,
щоб результат був завжди визначений.
Множина цілих чисел складається з множини
натуральних чисел 1, 2, 3,..., нуля і множини
від'ємних.цілих чисел -1, -2, -3.
Сума двох цілих чисел
т і п є цілим числом.
Якщо т, п будь-які цілі числа, то
існує єдине ціле число х, яке задовольняє рівняння
т+х=п. х — різниця чисел т і п.
Добуток двох цілих чисел є цілим числом х=аb.
Множина цілих чисел є
кільцем, тобто у множині цілих чисел виконуються три дії: додавання, віднімання та множення.
Найбільшим спільним дільником НСД(а,
b) =с називається найбільше натуральне число с, на яке діляться два дані числа а
і b без остачі.
Приклади: НСД(6, 3)=3; НСД(8, 4)=4;
НСД(22, 11)=11; НСД(12, 18)=6; НСД (1320, 408)=24.
Взаємно прості числа
Два числа називаються взаємно простими, якщо вони не мають
жодних спільних дільників, крім 1 і -1.
Приклади. 7 та 2 - це
взаєсно прості два числа, бо у них
тільки два спільні дільника -1 та 1.
Можна
довести, що числа 2m-1 і 2m+1 взаємно прості.
Довести, що якщо число n ділиться на кожне з двох взаємно простих чисел а і b, то воно ділиться
на їх добуток аb.
Найбільший спільний дільник записуємо так:
НСД (а, b)=с,
і він має властивості:
Якщо а:b ділиться
націло , де a та b натуральні числа, то НСД(а,
b)=b
Якщо а=bg+r, то НСД(а, b)= НСД(b, r).
Якщо m довільне
натуральне число, то НСД(аm, bm)= m*НСД(а, b).
Якщо НСД(а, b)=с, то НСД( a/c, b/c)=1.
НСК[а,
b] ділиться на НСД(а, b).
Якщо m ділиться на кожне з двох чисел а і
b, то m ділиться і на їх найменше спільне кратне НСК[а, b].
Чому може дорівнювати найменше спільне кратне
трьох чисел n-1, n, n+1 (де n — натуральне число)?
Довести, що частки від ділення найменшого
спільного кратного на дані числа є взаємно прості.
Найбільший дільник для взаємно простих
чисел дорівнює 1.
Якщо НСД(а,b)=1, то НСД(ас, b)= НСД(b, с).
Якщо НСД(а, b)=1 і ас/b, то с/b.
Якщо НСД(а,b)=1, с/а i с/b, то с=аb.
Завдання для
кмітливих та допитливих
Дослідження властивості парних і
непарних чисел
Розподілити тридцять тверджень на три групи:
·
перша група тверджень, які
завжди правильні на множині натуральних чисел;
·
друга група тверджень, які
завжди неправильні на множині натуральних чисел.
·
третя група тверджень, які
не входять до першої та до другої групи.
- Якщо число непарне, тоді його можна записати, як
добуток двох непарних чисел.
- Якщо число непарне, тоді його можна записати, як
суму парного і непарного чисел.
- Якщо число парне, тоді його можна записати, як
суму непарних чисел.
- Якщо число парне, тоді його можна записати, як
суму парних чисел.
- Якщо число ділиться на три, тоді сума його цифр ділиться на
дев’ять.
- Якщо число парне, тоді його можна записати, як
суму трьох непарних чисел.
- Якщо число непарне, тоді кожна цифра цього числа
непарна.
- Якщо число непарне, тоді сума цифр є число парне.
- Якщо число парне, тоді добуток його цифр є парним числом.
- Якщо натуральне число парне, тоді попереднє і
наступне число непарне.
- Якщо число кратне п’яти, тоді добуток цифр є
ненатуральним число.
- Якщо число парне, тоді добуток першої і останньої
цифр є число парне.
- Якщо число непарне, тоді добуток першої і
останньої цифр є число непарне.
- Якщо число парне, тоді сума першої і останньої
цифр є число парне.
- Якщо число кратне трьом, тоді добуток його цифр є
число кратне трьом.
- Якщо число кратне десяти, тоді добуток цифр є
число ненатуральне.
- Якщо число непарне, тоді його кількість цифр
непарна.
- Якщо число парне, тоді кількість його цифр є
число парне.
- Якщо число кратне чотирьом, тоді добуток цифр є
число непарне.
- Якщо число кратне шести, тоді добуток його цифр є
число парне.
- Якщо парне число має лише два ділиники, тоді сума
дільників цього числа непарна.
- Якщо число парне, тоді куб цього числа є число,
яке ділиться на 8.
- Якщо число парне, тоді куб цього числа є число
кратне восьми.
- Якщо число непарне, тоді квадрат цього числа є число
непарне.
- Якщо число складається з десяти різних цифр, тоді
сума цифр рівна 45.
- Якщо число складається з десяти різних цифр, тоді
сума цифр ділиться на дев’ять.
- Якщо число ділиться на кожну свою цифру, тоді
добуток його цифр рівний нулю.
- Якщо число ділиться на суму своїх цифр, тоді
добуток його цифр є число парне.
- Якщо число складається тільки з непарних цифр,
тоді добуток його цифр є непарне число.
- Якщо число складається тільки з парних цифр, тоді
сума квадратів його цифр є число кратне чотирьом.
- Якщо число парне, тоді сума усіх цифр цього числа
є парне число.
- Якщо число непарне, тоді сума цифр є число
кратне трьом..
- Якщо число парне, тоді сума цифр є число непарне.
- Якщо число непарне, тоді добуток цифр є число
парне.
- Якщо число парне, тоді його можна записати, як
суму непарних чисел.
- Якщо число непарне, тоді його можна записати, як
добуток двох непарних чисел.
- Якщо число парне, тоді його можна записати, як
суму парного і непарного чисел.
- Завжди парні
числа є наступними для чисел n, 3n + 3, 2n-1, 2n+1.
- Завжди ділиться натуральне число n(n+1) на 2.
- Завжди ділиться
добуток чотирьох послідовних натуральних чисел (n -1)n(n+1)(n+2) на 24.
- Добуток трьох непарних
послідовних чисел завжди ділиться на 3.
- Сума чотирьох
послідовних парних чисел ділиться
на два складених числа..
- Сума п'яти послідовних
натуральних чисел ділиться на два простих числа.
- Сума семи парних послідовних чисел не
ділиться на 4.
- Сума шести
послідовних непарних чисел не ділиться на 8.
- Сума чотирьох послідовних натуральних чисел може бути простим числом.
- Добуток
двох чисел дорівнює 150. Перше число упівтора рази більше другого. Тоді ці
числа парні.
- Додали два числа. Їх сума виявилась на 26 більше
від другого доданку. Тоді перший доданок рівний 6.
- Сума двох чисел
19, а їх різниця 9. Добуток
цих чисел 70.
- Цифрами
2, 4, 7, 9 не може закінчуватися такі суми: 1+2=…; 1+2+3=…; 1+2+3+4=…; 1+2+3+4+5=…; і так далі.
Цифрами 2, 3, 7, 8 не може
закінчуватися такі суми: 1+3=…; 1+3+5=…;
1+3+5+7=…; 1+3+5+7+9=…; і так
далі.
Запис натурального числа, відповідно
його властивостям
Розподілити двадцять п’ять тверджень на три групи:
·
перша група тверджень, які
завжди правильні на множині натуральних чисел;
·
друга група тверджень, які
завжди неправильні на множині натуральних чисел;
·
третя група тверджень, які
не входять до першої та до другої групи.
- Якщо натуральні
числа записується у вигляді 3m , 3m -1, 3m - 2, де
m − натуральне число,
то при діленні їх на 3 можна отримати остачі або 0, 1, 2.
- Якщо натуральні
числа записується у вигляді 7m , 7m+1, 7m+2, де
m − натуральне число,
тоді при діленні їх на 3
можна отримати остачі або 0,
1, 2.
- Якщо натуральні
числа записується у вигляді 8m , 8m+1, ,
де m − натуральне число, тоді
то при діленні їх на 2 можна
отримати остачі або 0, 1.
- Якщо натуральні
числа записується у вигляді m , m+1, m+2, де
m − натуральне число,
тоді сума цих натуральних
чисел ділиться на 3.
- Якщо натуральні
числа записується у вигляді m , m+1, m+2, де
m − натуральне число,
тоді добуток цих натуральних
чисел ділиться на 6.
- Якщо натуральні
числа записується у вигляді 7m , 7m+1, 7m+2, де
m − натуральне число,
тоді добуток цих натуральних
чисел ділиться на 6.
- Якщо натуральні
числа записується у вигляді 8m+3 , 8m+4, 8m+5, де
m − натуральне число,
тоді сума цих натуральних чисел не
ділиться на 12.
- Якщо десятицифрове число
містить усі десять цифр , то воно
ділиться на 3 і не ділиться на 9.
- Якщо натуральні
числа записується у вигляді 5m+1, 5m+2, 5m+4, 5m+3, де
m − натуральне число,
тоді сума цих натуральних чисел парна.
- Якщо натуральні
числа записується у вигляді m, m+1, m+2, m+3, m+4, де
m − натуральне число,
тоді сума цих натуральних
чисел парна.
- Якщо натуральні
числа записується
у вигляді m, m+1, m+2, m+3, m+4, де
m − натуральне число,
тоді сума цих натуральних чисел непарна.
- Якщо натуральні
числа записується у вигляді m, m+1, m+2, m+3, m-4, де
m − натуральне число,
тоді добуток цих натуральних
чисел ділиться на 30.
- Якщо натуральні
числа записується у вигляді 2m+1, 2m+2, де
m − натуральне число,
тоді добуток цих
натуральних чисел парний.
- Якщо натуральні
числа записується у вигляді 2m-2, 2m+2, де
m − натуральне число,
тоді добуток цих
натуральних чисел має дільник
8.
- Якщо натуральні
числа записується у вигляді 3m+2, 3m+3, 3m+4, де
m − натуральне число,
тоді добуток цих
натуральних чисел не ділиться на 6.
- Якщо п’ятицифрове число
містить усі парні цифри , то воно
ділиться на 3 і не ділиться на 9.
- Якщо п’ятицифрове число
містить усі непарні цифр , то воно
ділиться на 2 і ділиться на 9.
- Якщо натуральні
числа записується у вигляді 16m +12, 24m + 8, де
m − натуральне число, тоді
ці натуральні числа
мають спільний дільник 4.
- Якщо число парне, тоді
сума усіх цифр цього числа є парне число.
- Якщо число непарне,
тоді сума цифр є число кратне трьом..
- Якщо число парне, тоді
сума цифр є число непарне.
- Якщо число непарне,
тоді добуток цифр є число парне.
- Якщо число парне, тоді
його можна записати, як суму непарних чисел.
- Якщо число непарне,
тоді його можна записати, як добуток двох непарних чисел.
- Якщо число парне, тоді
його можна записати, як суму парного і непарного чисел.
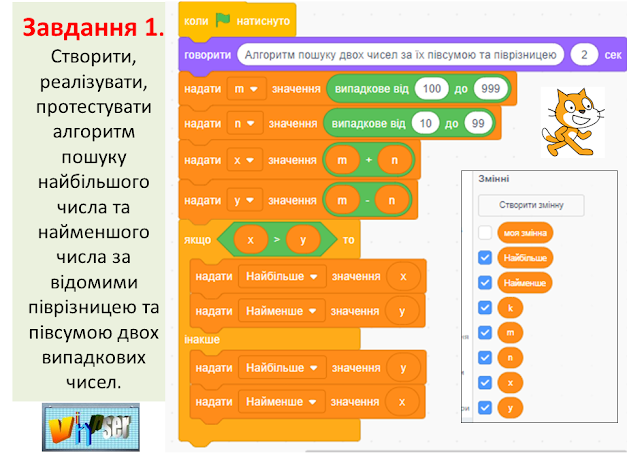
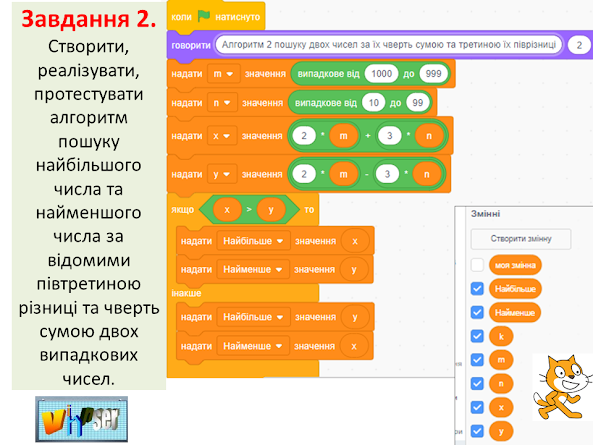
Практична частина
Наступні завдання
виконуються в середовищі програмування Scratch
Результати виконання практичної частина надіслати на електронну адресу учителя: vinnser@gmail.com
*********************
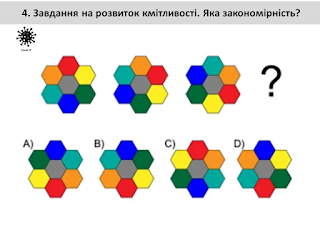
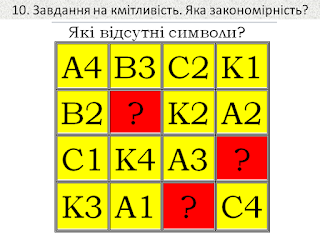
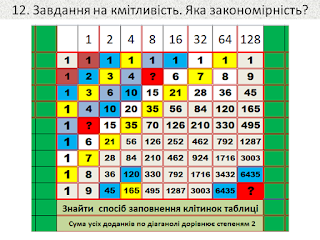
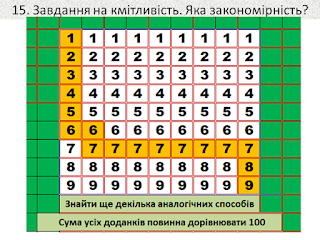
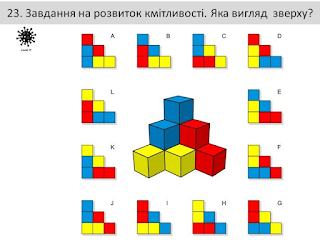
Завдання на розвиток кмітливості