Дистанційна освіта з інформатики в період лютого 2021 року
22.02.2021 - 28.02.2021
Тема: Створення та реалізація циклів з лічильником. Реалізація алгоритмів, що містять цикли. Діалоги і події в Скретч
Теоретична частина.
Опрацювати практичну частину на веб-сторінці:
https://inf5klas.blogspot.com
Для цього знайти на сайті:https://inf5klas.blogspot.com
1) знайти Практичну частину (пролистати сторіночку вниз)
і знайти умову: Завдання 1.
2) Уважно прочитати умову Завдання 1.
3) Відкрити програмний застосунок: Scratch.
4)У Scratch знайти вкладку «Образи» і відкрити цю вкладку,
5)Знайти кнопку «Імпортувати» і натиснути на неї лівою кнопкою миші
6) У папці «Animals» знайти спрайт, що являється рибкою.
5) Для активного спрайта рибка створити алгоритм у вкладці СКРИПТИ
6) натиснути зелений прапорець для виконання алгоритму.
7) Якщо в алгоритмі є помилки, то виправити їх порівнявши їх зі зразком.
8) Знову натиснути зелений кружечок для виконання алгоритму.
9) Активувати маленький білий квадратик із назвою «Сцена»
10) Знайти вкладку «Фони» а в ній знайти кнопку «Імпортувати» і натиснути на неї лівою кнопкою миші
11) У папці «Nature» знайти і обрати фон води «underwater» і активувати його кнопкою «Гаразд»
12)Результат проекту виконання скопіювати скріншотом, вставити в текстовий документ, його зберегти у файлі "Завдання 1".
13) Цей файл надіслати у листі на е-mail: vinnser@gmail.com
Аналогічно виконати:
завдання 2, завдання 3, завдання 4, завдання 5, завдання 6
Усі результати виконання алгоритмів надіслати файлами:
на е-mail: vinnser@gmail.com
Осмислюємо властивості алгоритмів на текстових компетентнісних завданнях:
Задача 1. Дано півсклянки води і півсклянки молока. Три ложки води долили до молока, а потім три ложки суміші знову перелили в склянку з водою. Чого виявилось більше ( у грамах) внаслідок цих переливань: суміші: води в молоці чи суміші: молока у воді?
Розв’язання: Порівну, бо скільки відлили молока, стільки ж долили води.
Задача 2. Три подруги одягли сукні різних кольорів. Одна − блакитну, друга − білу, і третя − зелену. Їхнє взуття було не таких самих кольорів, як сукні; тільки в Олі колір взуття був однаковий. Наталка була в зелених босоніжках. Сукня і взуття Валі не були білими. Хто і як був одягнений?
Розв’язання: Зрозуміло, що колір Валиного взуття блакитний. Отже, Оля була у білій сукні і білих босоніжках. Наталка одягла блакитну сукню, а Валя – зелену.
Задача 3. Скільки існує двоцифрових натуральних чисел, обидві цифри яких розташовані у зростаючому порядку?
Розв’язання: У другому десятку їх 8, у третьому десятку – 7, у четвертому десятку - 6, і так далі. 8+7+.....+ 2+1=36 двоцифрових чисел?
Задача 4. Довести, що серед 5 осіб принаймні двоє з них мають однакову кількість знайомих.
Розв’язання: Помістимо 5 осіб у „клітки” з номерами 0,1,2,3,4, де номер „клітки” відповідає кількості знайомих особи. Зауважимо, клітки з номерами 0 та 4 не можуть бути заповнені одночасно, бо якщо є особа, що не знайома ні з ким, тоді клітка під номером 4 порожня. Отже 5 осіб розміщені в чотирьох клітках. Принаймні дві особи знаходяться в одній клітці., тобто мають однакову кількість знайомих.
Задача 5. Для п’яти дипломатів є ключі в одній зв’язці. Скільки необхідно зробити спроб, щоб відімкнути три дипломати?
Розв’язання: Перенумеруємо усі дипломати. Першим із ключів в найгіршому випадку треба зробити 4 спроби. Якщо ключ не підійшов до 4 дипломатів, то цей ключ обов’язково відімкне п’ятий дипломат. Залишається 4 ключі та 4 дипломати. Другий ключ знайде свій дипломат у найгіршому випадку за 3 спроби, тоді третій ключ у найгіршому випадку відімкне за три спроби третій дипломат. Отже, щоб відімкнути три дипломати, потрібно 5+4+3=12 спроб.
Задача 6. Двоє по черзі розламують шоколадку 6x8. За один хід дозволяється зробити прямолінійний розлом будь-якої частини вздовж заглиблення. Програє той, хто не зможе зробити хід.
Розв’язання: Головне міркування: після кожного ходу кількість частинок збільшується рівно на 1. Спочатку був один шматок. В кінці гри, коли не можна зробити жоден хід, шоколадка розламана на маленькі частинки. А їх-48. Таким чином, гра буде тривати рівно 47 ходів, Останній, 47-й хід (також, як і всі інші ходи з непарними номерами), зробить перший гравець. Тому він в цій грі перемагає, причому незалежно від того, як він буде грати.
Задача 8. Є дві купи каменів по 7 в кожній. За хід дозволяється взяти
будь-яку кількість каменів, але тільки із однієї купи. Програє той, кому нема що брати.
Розв 'язування. В цій грі другий гравець перемагає за допомогою
симетричної стратегії: кожним своїм ходом він повинен брати
стільки ж каменів, скільки попереднім ходом взяв перший гравець,
але з іншої купи. Таким чином, у другого гравця завжди є хід.
Симетрія в цій задачі грунтується на рівності числа каменів в купах.
Задача 9. Є дві купки камінців: в одній -30, в другій - 20. За хід
дозволяється брати будь-яку кількість камінців, але тільки з одної купки.
Програє той, кому нема що брати.
Розв 'язування. Виграє перший. Першим ходом він зрівнює кількість
камшців в купках, після чого грає і перемагає за допомогою
симетричної стратегії: кожним своїм ходом він повинен брати
стільки ж каменів, скільки попереднім ходом взяв другий гравець,
але з іншої купи.
Практична частина
А тут лежить версія scratch4.30:
http://scratch.mit.edu/scratch2download/
Виконуємо лише чотири завдання на вибір
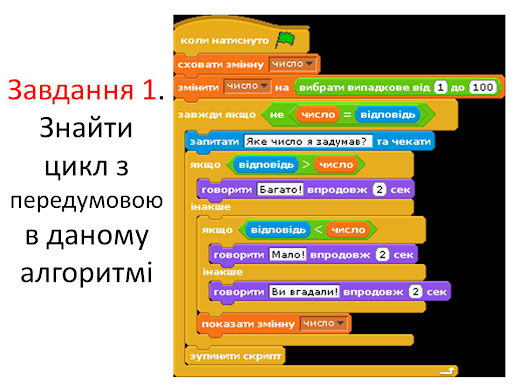
Завдання 1. Реалізувати даний алгоритм в середовищі Скретч.
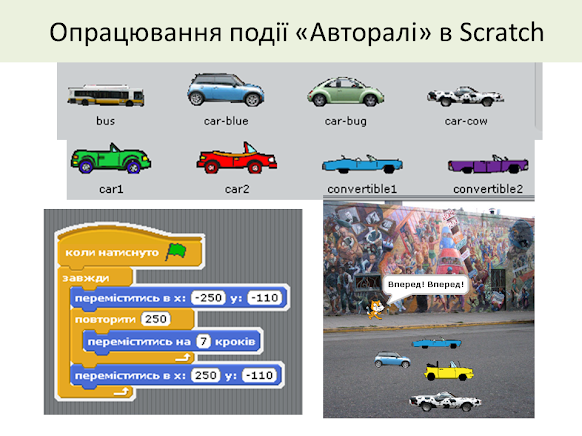
Завдання 2. Реалізувати даний алгоритм в середовищі Скретч.
Завдання 3. Реалізувати даний алгоритм в середовищі Скретч.
Завдання 4. Реалізувати даний алгоритм в середовищі Скретч.
Завдання 5. Реалізувати даний алгоритм в середовищі Скретч.
Завдання 6. Реалізувати даний алгоритм в середовищі Скретч.
Завдання 7. Реалізувати даний алгоритм в середовищі Скретч.
Результат виконаної практичної роботи - це чотири довільні файли( із кодами алгоритму та результатами виконання (скріншоти) алгоритму) надіслати вашому учителю на електронну скриньку:
vinnser@gmail.com (Сергій Петрович)
***************************************
Додаткові задачі для розвитку кмітливості























Немає коментарів:
Дописати коментар