13.12.2021-19.12.2021
Тема: Aлгоритми з
числовими типами даних
Теоретична частина
Двома основними правилами комбінаторики є:
Принцип суми. Якщо множина A містить m елементів, а множина B – n елементів, і ці множини не перетинаються, то A+B містить m+n елементів.
Принцип добутку. Якщо множина A містить m елементів, а множина B містить n елементів, то A*B містить m×n елементів, тобто пар (a;b).
Кількість елементів множини A будемо далі позначати |A|.
Ці правила мають також вигляд:
Принцип суми. Якщо об'єкт A можна вибрати m способами, а об'єкт B – n іншими способами, то вибір "або A, або B" можна здійснити m+n способами.
Принцип добутку. Якщо об'єкт A можна вибрати m способами і після кожного такого вибору об'єкт B може бути вибраним n способами, то вибір пари "A і B" в указаному порядку можна здійснити m×n способами.
Наведені правила очевидним чином узагальнюються на випадки довільних скінченних об'єднань множин, що попарно не перетинаються, та на скінченні декартові добутки.
При розв'язуванні математичних задач іноді використовують метод математичної індукції.
Принцип міркувань за індуктивним методом можна викласти в трьох пунктах.
Нехай існує послідовність тверджень Т1, Т2, Т3 , Т4, … причому:
1) Безпосередньою перевіркою впевнюються, що твердження Т1, Т2, Т3, Т4, …, Тк істинні;
2) Припускається, що деяке твердження Тк істинне, тоді на основі цього припущення доводиться, що наступне твердження Тк+1 також істинне.
3) Тоді стверджується, що всі твердження цієї послідовності істинні.
Такий спосіб міркувань називають методом математичної індукції. При цьому, доведення істинності твердження Т1, Т2, Т3, Т4, …, Тк, називають базою індукції, а доведення того, що з істинності твердження Тк випливає істинність твердження Тк+1, називають індукційним кроком.
Метод математичної індукції можна застосовувати не тільки для доведення, але і для означення послідовностей. Якщо ми означимо перший член послідовності, і, припустивши; що к-ий член вже означений, за допомогою нього означимо (к+1)-ий, то згідно принципу математичної індукції, вся послідовність буде означеною. Такий спосіб утворення послідовності називають рекурентним.
Існують й інші форми принципу математичної індукції. Іноді зручно починати індукцію не з доведення істинності Т1, а з доведення істинності деякого Тк. Принцип індукції еквівалентний такій аксіомі: в довільній непустій множині натуральних чисел є найменше.
Задачі Мудрої Сови:
1. Цеглина важить один кілограм плюс ще півцеглини. Скільки важить цеглина?
Відповідь: 2 кг. Адже півцеглини - це 1 кілограм, а півцеглини+півцеглини= ціла цеглина.
2. Цеглина важить 7 кілограм плюс ще півчверті цеглини. Скільки важить цеглина?
Відповідь: 8 кг. Адже півчверті цеглини - це 1/8 цеглини масою 1 кілограм,
бо 7/8 цеглини+1/8 цеглини= ціла цеглина=7+1=8 кг.
3. Цеглина важить півтора кілограми плюс ще третина цеглини. Скільки важить цеглина?
Відповідь: 2кг 250 г. Адже третина цеглини - це 1/3 цеглини масою 750 грам,
бо 2/3 цеглини+1/3 цеглини= ціла цеглина=1 кг 500 г+ 750 г= 2кг 250 г.
4. Три подруги одягли сукні різних кольорів. Одна − блакитну, друга − білу, і третя − зелену. Їхнє взуття було не таких самих кольорів, як сукні; тільки в Олі колір взуття був однаковий. Наталка була в зелених босоніжках. Сукня і взуття Валі не були білими. Хто і як був одягнений?
Розв’язання: Зрозуміло, що колір Валиного взуття блакитний. Отже, Оля була у білій сукні і білих босоніжках. Наталка одягла блакитну сукню, а Валя – зелену.
5. Скільки існує двоцифрових натуральних чисел, обидві цифри яких розташовані у зростаючому порядку?
Розв’язання: У другому десятку їх 8, у третьому десятку – 7, у четвертому десятку - 6, і так далі. 8+7+.....+ 2+1=36 двоцифрових чисел?
6. Довести, що серед 5 осіб принаймні двоє з них мають однакову кількість знайомих.
Розв’язання: Помістимо 5 осіб у „клітки” з номерами 0,1,2,3,4, де номер „клітки” відповідає кількості знайомих особи. Зауважимо, клітки з номерами 0 та 4 не можуть бути заповнені одночасно, бо якщо є особа, що не знайома ні з ким, тоді клітка під номером 4 порожня. Отже 5 осіб розміщені в чотирьох клітках. Принаймні дві особи знаходяться в одній клітці., тобто мають однакову кількість знайомих.
7. Дано порожню клітинкову таблицю 3х3. Заповнити її всіма цифрами, крім 0, так щоб по горизонталям, по вертикалям, по діагоналям була однакова сума. Тобто, треба створити магічний квадрат розміром 3х3 із чисел 1,2,3,4,5,6,7,8,9.
Розв'язування. 1+9=2+8=3+7=6+4=10. Середнє серед цих цифр, це 5.
Зрозуміло, що треба додати усі цифри 1+2+3+4+5+6+7+8+9= ? так, отримаємо 45.
Це число 45 розділити на 3 отримати 15. Отже сума по горизонталям, по вертикалям, по діагоналям рівна 15. Середнє серед цих цифр, це 5, повинна стояти в центральній клітинці.
Тоді в сусідній з нею клітинках повинні стояти непарні цифри: 1+9=3+7. В кутових клітинках повинні стояти парні числа: 6+4=2+8.
Знайшовши один такий набір можна отримати ще вісім таких квадратів за допомогою повороту навколо центральної клітинки.
Задача 8-а. Чи можна розміняти 25 грн за допомогою десяти купюр вартістю 1, 3 та 5 грн?
Розв'язання цієї задачі грунтується на простому спостереженні: сума парної кількості непарних чисел є парною: 1+3=4; 1+3+5+1=10. Узагальнення цього факту виглядає так: парність суми кількох чисел залежить лише від парності числа непарних доданків: якщо кількість непарних доданків є (не)парна, то і сума також є (не)парною. Отже, розміняти 25 грн не можна, бо десять довільних непарних чисел завжди дають парну суму, проте 25 - це непарне число. Відповідь: не можна!
Задача 8-б. У заданій неправильній рівності ХІ + І = Х не треба перекладати сірники, але як зробити цю правильної.
Розв’язання. Перевернути її знизу вгору. Отримаємо, Х=І+ІХ.
Задача 9. У заданій неправильній рівності Х- І = І треба перекласти сірник, але так, щоб зробити цю рівність правильної.
Розв’язання. Знак мінус поставити одиницею на початок. Отримаємо множення одиниць. І Х І = І.
Задача 10. У заданій буквеній рівності ПЛЯЖ+ШЛЯХ=ХВИЛЯ треба замінити букви цифрами, але так, щоб зробити цю рівність правильної і при цьому однаковим буквам відповідають рівні цифри, а різним буквам відповідають нерівні цифри.
Розв’язання. 3894+6895=10789, або 5687+4681=10368.
Задача 11. У заданій буквеній рівності БОРЩ+КОРЖ=ОБІД треба замінити букви цифрами, але так, щоб зробити цю рівність правильної і при цьому однаковим буквам відповідають рівні цифри, а різним буквам відповідають нерівні цифри.
Розв’язання. 3651+2657=6208, 2657+ 3651=6308.
Задача 12. У заданій буквеній рівності СИР+РИС=ЇЖА треба замінити букви цифрами, але так, щоб зробити цю рівність правильної і при цьому однаковим буквам відповідають рівні цифри, а різним буквам відповідають нерівні цифри.
Розв’язання. 273+372=645, або 293+392=685.
Задача 13. У заданій буквеній рівності РАК+БУГ=РІКА треба замінити букви цифрами, але так, щоб зробити цю рівність правильної і при цьому однаковим буквам відповідають рівні цифри, а різним буквам відповідають нерівні цифри.
Розв’язання. 152+973=1025.
14. Шість однакових діжок вміщують 28 відер води. Скільки відер води можуть вмістити таких 15 діжок?
Розв’язання. 28:2=14 відер вміщують три діжки(6:2=3).
14·5=70 відер води вміщують 15 діжок(3·5=15).
Відповідь: 70 діжок.
Практична частина
Результати виконання практичної частина надіслати на електронну адресу
учителя: vinnser@gmail.com
*************************
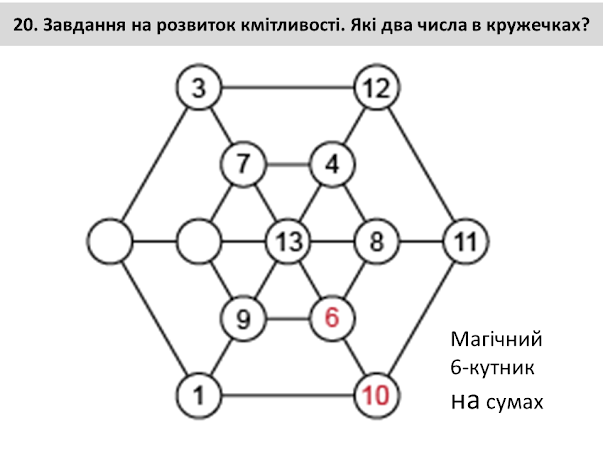
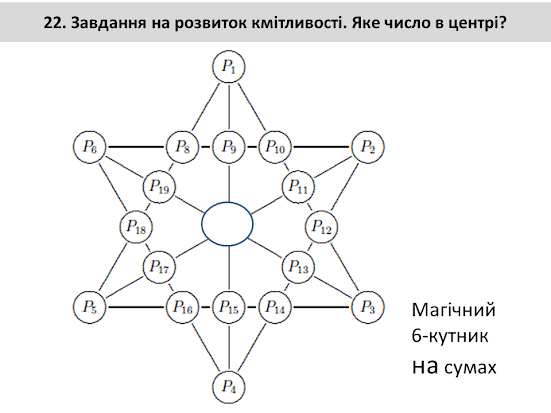
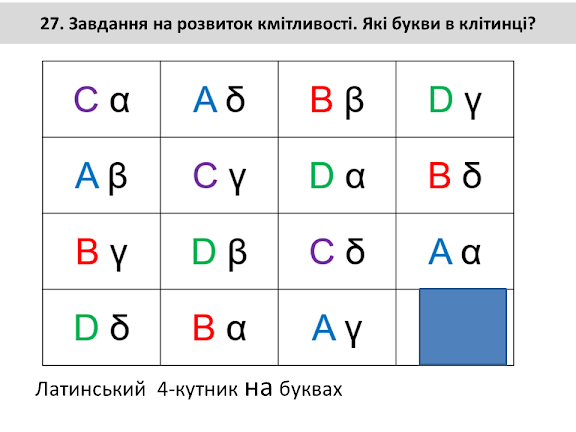
Задачі на розвиток кмітливості